How does Spotify Codes Work?

Spotify codes

I love music and I spend most of my day listening to songs. Spotify codes caught my eye from past some days, so I went on finding how do they work. I thought I should share this journey, how even the maker of Spotify codes Ludvig Strigeus,(also the maker of utorrent)was involved.

This is the sequence of the “Girl Of My Dreams” Spotify code:

Spotify barcode

Spotify Codes are like QR-codes that can be generated to easily share Spotify songs, artists, playlists, and users.

Spotify URIs

Spotify URIs (Uniform Resource Identifiers). Different pieces of media (artists, albums, songs, playlists, users) all have a URI.

A URI is a code you can use for embedding and searching within the Spotify app. Spotify URI codes look like this:

spotify:user:spotify:playlist:37i9dQZF1DXcBWIGoYBM5M.

The 22 characters are the numbers 0-9, characters a-z and A-Z. This means there are 10 + 26 + 26 = 62 possibilities for each character (almost Base64). So the potential number of Spotify URIs is 62^22 which is equal to 2.7e39 which is a veryyy longgg digit so Spotify is not running out of these any time soon.

Spotify Codes When the bars are sorted by height you can see that there are 8 discrete heights that they fall into.

In this function I use scikit-image to calculate the sequence of bar heights from a logo.

 1
 2
 3
 4
 5
 6
 7
 8
 9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
27
28
29
30
31
32
33
34
35
36


from skimage import io
from skimage.measure import label, regionprops
from skimage.filters import threshold_otsu
from skimage.color import rgb2gray


def get_heights(filename: str) -> list:
    """Open an image and return a list of the bar heights.
    """
    # convert to grayscale, then binary
    image = io.imread(filename)
    im = rgb2gray(image)
    binary_im = im > threshold_otsu(im)

    # label connected regions as objects
    labeled = label(binary_im)

    # get the dimensions and positions of bounding box around objects
    bar_dimensions = [r.bbox for r in regionprops(labeled)]

    # sort by X
    bar_dimensions.sort(key=lambda x: x[1], reverse=False)

    # the first object (spotify logo) is the max height of the bars
    logo = bar_dimensions[0]
    max_height = logo[2] - logo[0]
    sequence = []
    for bar in bar_dimensions[1:]:
        height = bar[2] - bar[0]
        ratio = height / max_height
        # multiply by 8 to get an octal integer
        ratio *= 8
        ratio //= 1
        # convert to integer (and make 0 based)
        sequence.append(int(ratio - 1))
    return sequence

get_heights [0, 5, 1, 2, 0, 6, 4, 3, 7, 1, 6, 7, 7, 7, 7, 3, 1, 6, 3, 7, 0, 7, 0]

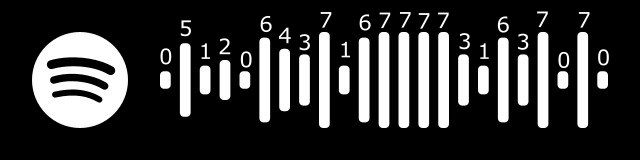
spotify code with heights labeled

According to StackOverflow discussion, The barcode consists of 23 bars, of which only 20 contain information. This means that there are 8^20 pieces of information that can be encoded into the code.

A media reference is first generated by Spotify for a Spotify URI(link to URI para). The media reference is what gets encoded into the barcode and links the barcode to the URI. Spotify maintains a database of media references to URI mappings. Media references let Spotify track which codes are scanned, enable them to theoretically re-map codes, and just look better when encoded(which they successfully made it look, omg I love the aesthetics)

Simple no, no it isn’t. There is a lot more which goes on in the background. Problems :

Big to small barcode URIs to barcode (The weird thing about this is the amount of information in the URI and the Spotify code do not match up.)
Error correction
String encryption

So to solve these problems,codes are then send through CRC Calculation, Convolutional encoding, and reversing (Decoding).
Gray-scale (gray codes)was one of techniques in which ordering of the binary numeral system such that two successive values differ in only one bit, omg stop imaging I know what you all are thinking greyscale disease from Game of thrones, well that is not what is used here.

For example, the representation of the decimal value “1” in binary would normally be “001” and “2” would be “010”. In Gray code, these values are represented as “001” and “011”. That way, incrementing a value from 1 to 2 requires only one bit to change, instead of two.

The media reference can be expressed as a 37 bit binary number:

1

57639171874 -> 0100010011101111111100011101011010110

CRC Calculation

This is very it got interesting for me, I had computer networks this semester and we learnt all these concepts in theory. I wanted to see how these are actually used and implemented.

Cyclic redundancy check is a method of detecting accidental changes/errors in the communication channel and bits are generated for the media reference. A CRC calculates check bits to verify the integrity of the data.

In simple words its a error checking algorithm, for example if a receiver receviecs a packet of data from sender, how will it know the data was correct and bits are not interchanged during transmission. So transmitter sends the original data, and attaches a fixed number of check bits, which are derived from the data bits by some deterministic algorithm(here CRC). If only error detection is required, a receiver can simply apply the same algorithm to the received data bits and compare its output with the received check bits if the values do not match, an error has occurred at some point during the transmission.

Spotify uses CRC-8 with the following generator:

1

x^8 + x^2 + x + 1

Which gives us the following polynomial when fully written out:

1
2


1x^8 + 0x^7 + 0x^6 + 0x^5 + 0x^4 + 0x^3 + 1x^2 + x + 1
[1, 0, 0, 0, 0, 0, 1, 1, 1]

The CRC is calculated by following these steps:

Pad with 3 bits on the right

1

01000100 11101111 11110001 11010110 10110000

Reverse bytes

1

00100010 11110111 10001111 01101011 00001101

Calculate CRC as normal (highest order degree on the left)

1

11001100

Reverse CRC

1

00110011

Invert check

1

11001100

Finally append to step 1 result

1
2


01000100 11101111 11110001 11010110 10110110 01100
|----------Media Ref--------------------||--CRC--|

Here is a simple version of a crc calculator (step 3):

 1
 2
 3
 4
 5
 6
 7
 8
 9
10
11


def crc(data, polynomial):
    # xor the data with the polynomial at each occurrence of 
    # a 1 in the data. Return the remainder as the checksum.
    n = len(polynomial) - 1
    initial_length = len(data)
    check_bits = data + [0] * n
    for i in range(initial_length):
        if check_bits[i] == 1:
            for j, p in enumerate(polynomial):
                check_bits[i + j] = check_bits[i + j] ^ p
    return check_bits[-n:]

We can use the check bits to verify that the contents of the data match what was intended by the “sender”:

 1
 2
 3
 4
 5
 6
 7
 8
 9
10
11
12


def check_crc(data, polynomial, check_bits):
    full_data = data + check_bits
    for i in range(len(data)):
        if full_data[i] == 1:
            for j, p in enumerate(polynomial):
                full_data[i + j] = full_data[i + j] ^ p
    return 1 not in full_data
data = [0,0,1,0,0,0,1,0,1,1,1,1,0,1,1,1,1,0,0,0,1,1,1,1,0,1,1,0,1,0,1,1,0,0,0,0,1,1,0,1]
check = [1,1,0,0,1,1,0,0]
poly = [1,0,0,0,0,0,1,1,1]
print(check_crc(data, poly, check))
# True

Convolutional encoding

These 45 bits are then convolutionally encoded. Convolutional codes add redundancy to data to make it possible to decode the data if errors are introduced during transmission.

Resources to learn more these MIT lecture notes

Spotify’s patent

High-Rate Punctured Convolutional Codes for Soft Decision Viterbi Decoding

Convolutional Codes and State Machine View/Trellis (MIT Slides)

The Error Correcting Codes Page

Reed-Solomon Codes and the Exploration of the Solar System

The code can then be transformed into an error correcting code, such as a forward error correcting code. The forward error correction used can, for example, be a convolutional code.

Tail biting

Before we start calculating the parity bits, we must prepend stream with last 6 bits of data:

1
2
3
4
5


01000100 11101111 11110001 11010110 10110110 01100
                                           |-----|

001100 01000100 11101111 11110001 11010110 10110110 01100
|----|

Another approach would be to prepend 0s to the input, but Spotify chose to go with this tail-biting method.

Encoding

We can focus on one generator at a time. Below is a step by step walkthrough of how the parity bits are generated for g0. I reversed the polynomial because it is easier to display right to left in the example.

 1
 2
 3
 4
 5
 6
 7
 8
 9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
27
28
29


Bit #0
001100010001001110111111110001110101101011011001100
1101101 <- generator polynomial (mask)
-------
0001000 = 1 (xor the bits together)

Bit #1
001100010001001110111111110001110101101011011001100
 1101101 <- generator polynomial (mask)
 -------
 0100001 = 0 (xor the bits together)

Bit #2
001100010001001110111111110001110101101011011001100
  1101101 <- generator polynomial (mask)
  -------
  1100000 = 0 (xor the bits together)

Bit #3
001100010001001110111111110001110101101011011001100
   1101101 <- generator polynomial (mask)
   -------
   1000100 = 0 (xor the bits together)

Bit #4
001100010001001110111111110001110101101011011001100
    1101101 <- generator polynomial (mask)
    -------
    0001000 = 1 (xor the bits together)

Continue this to the end of the stream of input bits:

1
2
3
4
5


Bit #45
001100010001001110111111110001110101101011011001100
                                            1101101 <- generator polynomial (mask)
                                            -------
                                            1001100 = 1 (xor the bits together)

The result of encoding with the first generator, g0:

1

100011100111110100110011110100000010001001011

The result of encoding with g1:

1

110011100010110110110100101101011100110011011

Here is a (naive) algorithm for calculating the parity bits:

 1
 2
 3
 4
 5
 6
 7
 8
 9
10
11
12
13
14
15
16
17


def encode(bits: List[int], polynomial: List[int], tail_bite=False):
    """Convolutionally encode the stream of bits using the generator polynomial.
    If tail_bite == True, prepend the tail of the input. Otherwise use 0s to fill.
    """
    if tail_bite:
        tail = bits[-(len(polynomial) - 1):]
    else: 
        tail = [0 for i in range(len(polynomial) - 1)]
    full = tail + bits
    polynomial.reverse() # Reverse since we're working the other direction
    parity_bits = []
    for i in range(len(bits)):
        parity = 0
        for j in range(len(polynomial)):
            parity ^= full[i + j] * polynomial[j]
        parity_bits.append(parity)
    return parity_bits

These two parity bit sequences are then interleaved (abab…):

1
2
3
4


1 0 0 0 1 1 1 0 0 1 1 1 1 1 0 1 0 0 1 1 0 0 1 1 1 1 0 1 0 0 0 0 0 0 1 0 0 0 1 0 0 1 0 1 1
 1 1 0 0 1 1 1 0 0 0 1 0 1 1 0 1 1 0 1 1 0 1 0 0 1 0 1 1 0 1 0 1 1 1 0 0 1 1 0 0 1 1 0 1 1
result:
110100001111110000101110111100110100111100011010111001110001000101011000010110000111001111

Puncturing

At this point we have gone from 45 bits to 90 bits. The rate of this convolutional code is 1/2 (one input bit results in 2 parity bits).

A rate of 1/2 is actually somewhat low for this application (see this article about QR code rates). The rate can be increased by “puncturing” the code. We can remove every third bit to increase the rate to 3/4:

1
2
3
4


110100001111110000101110111100110100111100011010111001110001000101011000010110000111001111
11 10 00 11 11 00 10 11 11 10 11 10 11 10 01 01 11 00 11 00 00 10 01 00 01 11 00 11 00 11
result:
111000111100101111101110111001011100110000100100011100110011

This is equivalent to puncturing the two parity bit sequences with the patterns 101 and 110 before interleaving. Puncturing is a nice, simple way to increase the rate of your code after you estimate the frequency of expected errors.

Permutation

Spotify then shuffles the data to spread out errors when a whole bar is lost:

A shuffling process may be used to spread out the potential errors (e.g., if a whole bar/distance is missing). Instead of having the encoded bar lengths be consecutive, the lost bits are non-consecutive in the code word. This improves the chances for the forward error correction to work when a whole bar or distance is lost. Thus to scan the optical code, after the lengths of the found bars are converted into bits with certainties, the bits are shuffled back into the right order.

source

The bits are permuted by choosing every 7th bit (modulo 60) from the input.

1
2
3


def permute(bits, step=7):
    for i in range(len(bits)):
        yield bits[(i * step) % len(bits)]

Input and result:

1
2


111000111100101111101110111001011100110000100100011100110011
111100110001110101101000011110010110101100111111101000111000

Map to bar heights

Finally, map the bits to bar heights between 0 and 7 using gray code:

Decimal	Binary	Gray
0	000	000
1	001	001
2	010	011
3	011	010
4	100	110
5	101	111
6	110	101
7	111	100

1
2


111 100 110 001 110 101 101 000 011 110 010 110 101 100 111 111 101 000 111 000
 5   7   4   1   4   6   6   0   2   4   3   4   6   7   5   5   6   0   7   0

Three additional bars are added as reference points at the start, end, and 12th position:

1

[0]5741466024[7]3467556070[0]

Decoding

Let’s reiterate why we went through the process of calculating the CRC and convolutionally encoding the data:

Convolutional codes allow us to correct for errors in a message by sending “redundant” bits with the message
The CRC lets the client check the validity of the decoded Spotify code. If the check bits are not correct, the client can scan the code again. When they are correct, then the client can ping Spotify’s servers. As Ludvig says, “I chose to include a CRC to let the client have a way to more easily discard invalid codes without a backend roundtrip.”

The process of transforming an image of a Spotify code to a media reference follows approximately the same steps as encoding in reverse. However, there is a much more happening while decoding a convolutional code.

Как спрятать мусор в базе Spotify и превратить это в квест (How to hide trash in Spotify database and turn it into a quest)

Cracking Spotify Codes and making a quest out of it

Spotify’s bug bounty. Great idea, but it was possible to pass in the bug bounty

Spotify codes#

Spotify URIs#

CRC Calculation#

Convolutional encoding#

Tail biting#

Encoding#

Puncturing#

Permutation#

Map to bar heights#

Decoding#